
 |
Intermediate Macroeconomics | |
5. The Keynesian Model |
For 150 years economic theory was built on the foundation laid with the publication of Scottish economist Adam Smith's book, An Inquiry into the Nature and Causes of the Wealth of Nations, in 1776. Smith and the classical economists that followed believed that governments could be their own worst enemies when it came to the economy. With laissez-faire (hands-off) government policies the economy would better achieve the goals of price stability, full employment, and economic growth.
Classical economic theory was not much help in the 1930s as the world economies became swamped by the Great Depression. By 1932 the U.S. unemployment rate has passed 20 percent. Between 1929 and 1932 U.S. real GDP has fallen by over 25 percent. Something had to be done and classical economic theory at that time offered no solutions. The classical economists believed that prices, wages and interest rates would adjust "as if led by an invisible hand" to return the economy to full employment and economic growth.
The tide turned as John Maynard Keynes led a revolution in macroeconomic thought that began with his book, General Theory of Employment, Interest, and Money, which came out in 1936. Prices, wages, and interest rates were not declining as needed to stimulate demand and the economy. Keynes presented a new macroeconomic theory that asked what could government do when prices, wages, and interest rates were fixed, or "sticky". The solution, as we will see in this chapter, was active government fiscal policy. Tax cuts or increased government spending were needed for the economy to recover. This major departure from classical economic laissez-faire policy was evidently warmly received by the Roosevelt administration and the New Deal was born. The government began building roads, parks, and dams to put people to work. Of course, the final government spending push came with the start of World War II, but that's another story.
The foundation of Keynesian macroeconomic theory is that prices, wages, and interest rates are fixed. Prices and wages are directly related because firms could not lower product prices if wages were not lowered. Classical economic theory suggested that high unemployment rates would lead to lower wage rates, which would lead to lower prices, which would lead to higher demand because of the increased purchasing power of existing wealth. But Keynes observed that wages were not falling (actually there was a decline in the average price level during the early 1930s but evidently not enough to matter). Keynes could not apply an economic theory to explain why those out of work were unwilling to accept a lower wage in order to get a job. He simply accepted it as an unexplained socioeconomic fact of life and built a theory around the assumption that prices and wages were rigid.
Interest rates are a different story. Classical theory suggests that during a recession or depression interest rates should fall, which would stimulate consumption and investment spending. Keynes observed that if interest rates were already near zero how could they go any lower. Moreover, even if interest rates could decline further why would that lead to an increase in investment? With factories running well below capacity because of the Depression, why build new production plants?
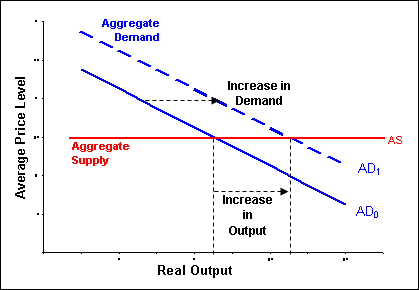
The assumption that prices and interest rates are fixed implies the aggregate supply curve is flat as shown in Figure 5-1. Consequently, any change in aggregate supply (i.e., a rightward or leftward shift) will have no effect on the economy. Aggregate demand is the driving force in Figure 5-1. On the supply side firms simply increase or reduce production at the constant market price to meet the level of demand.
We begin with an accounting definition for aggregate expenditures because this is the heart of the Keynesian model. We will convert the accounting identity for aggregate expenditures into a model by first proposing an equilibrium condition in which aggregate output equals aggregate expenditures. Second, we will propose a behavioral equation for consumption in which people vary their consumption spending based on their level of income. By doing this we convert consumption from the level of actual spending in the accounting equation to the desired level of spending in our model. We can then build a simple model that will reveal perhaps the most important feature of the Keynesian theory - spending multipliers. A $1 increase in (government) spending will lead to a larger increase in aggregate output because of the multiplier process. Finally we will expand our representation of government to include different forms of taxes and spending to refine the multiplier for government fiscal policy.
![]()
Total spending on goods and services in the economy is the sum of four components: consumption, investment, government spending, and net exports. Equation (1) is an accounting identity that corresponds to the calculation of a country's GDP. We call this aggregate expenditure rather than aggregate demand because prices are assumed to be fixed. Somewhere and sometime it became the convention in economics to use the term aggregate demand only in a graph of price versus quantity, in which prices are variable.
| AE = C + I + G + NX | (1) |
Since prices are assumed constant in the Keynesian model there is no need to distinguish between between nominal and real expenditure or income.
![]()
The first step in converting the accounting identity for aggregate expenditures into a macroeconomic model is to propose an equilibrium condition. The economy is in equilibrium when aggregate output is equal to aggregate expenditures. Firms are selling as much as they produce and households are buying the amount they want to purchase.
| Y = AE | (2) |
We make the simplifying assumption that income is the same as aggregate output. Put simply, the increase in wealth (i.e., income) of labor and the owners of capital (stock and bondholders) corresponds to the total output produced.
In the traditional classical macroeconomic theory, equilibrium always occurs at full employment output. The economy may be below its potential or full employment level at a point in time but since that cannot represent an equilibrium it cannot stay there. From a disequilibrium condition the economy will return to full employment equilibrium through adjustment of prices, wages, and interest rates.
In the Keynesian model with fixed prices we can have an equilibrium when the economy is operating below its potential of full employment. The implication during the Great Depression was that the economic depression could continue since it represents a possible equilibrium. The government must step in to force the economy to a new equilibrium at full employment.
When the economy is not in equilibrium aggregate output does not equal aggregate expenditures. Firms are producing more or fewer goods than households are buying. What we will see in a disequilibrium condition is that inventories are either building (output exceeds expenditures) or declining (output is less than expenditures). In the classical model when there is undesired inventory build or draw, firms will lower or raise prices to eliminate the imbalance. In the Keynesian model with fixed prices firms will simply reduce or increase production without changing prices.
![]()
The relationship between consumption and income is described by the consumption function. The consumption function represents the "planned" or "desired " level of consumption for a given level of income. Other non-income factors that may affect consumption such as the weather, wealth, interest rates, and prices are assumed constant.
| C = C0 + c • Y | (3) |
Consumption is made up of two components: autonomous consumption, C0, which is consumption that is independent of the level of income, and income induced consumption, c • Y, that does depend on the level of income.
When income is zero total consumption is equal to the autonomous level of consumption. You might think of autonomous consumption as the minimum level of consumption necessary to survive (often called the "subsistence" level). Even if you are unemployed you still have to eat and hopefully sleep under a roof. You still consume food and housing. Autonomous consumption does not play a major role in our analysis of the Keynesian model that follows. However, it does become important when we investigate consumption in detail in a later chapter.
The income induced part of consumption is critical to the Keynesian model. As income increases consumption rises by a constant fraction of that increase. The change in consumption for every $1 change in income is called the marginal propensity to consume, or MPC. If the MPC is 0.8, a $1 increase in income raises consumption by $0.80. A $1,000 increase in income raises consumption by $800.
| Marginal propensity to consume - the amount that consumption changes in response to an incremental change in disposable income. It is found by dividing the change in consumption by the change in disposable income that produced the consumption change. |
| MPC = | change in consumption change in income |
We can use some simple calculus to show that the MPC is equal to the coefficient c in the consumption equation. Take the derivative of the consumption function with respect to income and we get the marginal propensity to consume out of income:
| MPC = dC = c dY |
(4) |
The consumption function is a simple linear equation that is graphed as a straight line in Figure 5-2 with the intercept on the vertical (expenditure) axis equal to the autonomous component, C0, and the slope equal to the marginal propensity to consume, c. When income is zero, total consumption is equal to the autonomous level of consumption. If the marginal propensity to consume is 0.9 then the slope of the consumption function equals 0.9. For every $1 increase in income there is a $0.90 increase in consumption.

![]()
There are three components of aggregate expenditure we still need to define: investment, government spending, and net exports. We assume that all three components are autonomous, not determined by any variable within the model. In particular, we assume these three components are independent of the level of income.
| Autonomous Spending - spending that is determined outside the model (independent of level of income and other variables). |
| Investment Spending: | I = I0 | (5) |
| Government Spending: | G = G0 | (6) |
| Net Exports: | NX = NX0 | (7) |
Assuming that investment spending is autonomous is obviously a very strong assumption. In normal economic conditions we should expect investment spending to be a function of interest rates, wealth, income and other variables (we discuss investment in more detail in a later chapter). But, as we mentioned in the opening section, Keynes observed that we should not expect investment to respond to changes in income or the interest rate in the short run when capacity is under utilized.
Assuming government spending is independent of income is more of a problem. Income tax revenues rise when income increases. When government revenues go up, government spending usually increases. We will only partially resolve this problem when we introduce income tax in section 7 below. But we still don't allow government spending to increase with income. Keynes advocated that government should be more fiscally responsive and responsible. During a recession when tax revenues decline the government should not cut spending but rather do the opposite, otherwise the recession would get worse. The government should run a deficit during the recessionary phase of the business cycle. When income rises as the economy recovers, the government should refrain from increasing spending but run a budget surplus to pay off the earlier deficit.
![]()
The components of the Keynesian model (the equilibrium condition and the aggregate expenditures equation) have been established. Note that we have really only defined spending. This characterizes the Keynesian model as strictly a model of demand. The supply side is essentially ignored. Firms simply increase or reduce output to meet the level of demand at the fixed price level. The aggregate supply curve is flat at the fixed price level and only shifts in spending result in changes in aggregate economic output.
This leads us to two basic questions on spending and the economy:
What happens to total output and national income if there is a change in autonomous spending (e.g., government spending)?
If the economy is in a recession, how much of an increase in autonomous spending is needed to increase total output and income to the level of full-employment output?
To answer these questions we just need to set up and solve our model, which we can do with some simple algebra.
First, we are given the following equations about how the economy works, which have been described above as equations (1), (3), (5), (6), and (7):
| AE = C + I + G + NX |
| C = C0 + c • Y | ||
| I = I0 | ||
| G = G0 | ||
| NX = 0 (for convenience) |
The solution of the model follows four steps.
Step 1. Substitute the equations for the four spending components into the aggregate expenditure equation (1):
| AE = C0 + c • Y + I0 + G0 |
The aggregate expenditures function in Figure 5-3 looks identical to the consumption function in Figure 5-2, except that it has shifted up by I0 + G0.

Step 2. Apply the equilibrium condition, equation (2):
| Y = AE |
The equilibrium condition is drawn in Figure 5-4 as the dashed line starting at the origin. This equilibrium line (often called the "45 degree line") identifies all possible points of equilibrium where aggregate expenditures equals total income.

We could use Figure 5-4 to characterize how the economy would work. For example, an increase or decrease in autonomous spending (the intercept) would shift the aggregate expenditure line up or down, which would lead to an increase or decrease in national income. If the economy is in a recession so that national income is less than it would be at full employment all we have to do is increase autonomous government spending to shift the aggregate expenditure line up. But we have to do more than that. We have to be able to say how much. To do that we need to stick with the algebra and develop an equation into which we can plug some numbers and come up with specific recommendations. So, we move on to Steps 3 and 4 to solve the model.
Step 3. Substitute AE from Step 1 into the equilibrium condition in Step 2:
| Y = (C0 + I0 + G0) + c • Y |
Step 4. Collect the Y terms on the left hand side and solve for national income, Y.
| Y - c • Y = C0 + I0 + G0 |
| (1 - c) • Y = C0 + I0 + G0 |
| Y = 1 • (C0 + I0 + G0) 1 - c |
(8) |
Equation (8) reveals what is perhaps the most important feature of the Keynesian model: the autonomous spending multiplier. The autonomous spending multiplier is the derivative of the income equation (8) with respect to autonomous spending.
| Autonomous spending multiplier = | 1 1 - c |
= | 1 1 - MPC |
The autonomous spending multiplier tells us how much total output or income increases when there is a one dollar increase in autonomous expenditures. For example, if the marginal propensity to consume, c, equals 0.8, the autonomous spending multiplier equals 5.0. If autonomous government spending, G0, increases by $1, national income, Y, increases by $5.
| Autonomous Spending Multiplier - the amount by which output and national income change when autonomous aggregate expenditures change by one unit. |
We get the "big bang for the buck" multiplier effect because of consumption. Let's say the government increases spending by $100. That spending is income to someone. If the marginal propensity to consume is 0.8, whoever gets the $100 turns around and spends $80 of that income (0.8 x $100 = $80). That $80 spending is income to someone else. That person then spends $64 of that $80 income (0.8 x $80 = $64). That $64 is income to someone, and so on. National income has increased by the original $100 plus the subsequent spending of $80 and then $64 and then... The cumulative increase in national income according to the multiplier is $500.

The larger the marginal propensity to consume, c, the larger the multiplier as we can see in Table 5-1. In Figure 5-5, a larger marginal propensity to consume means a steeper aggregate expenditure curve. A given increase in autonomous spending leads to a larger increase in national income if the MPC is larger and the aggregate expenditure curve is steeper.
| Table 5-1. The MPC and Autonomous Consumption Multiplier | |
| Marginal Propensity to Consume |
Autonomous Spending Multiplier |
| 0.5 | 2.0 |
| 0.6 | 2.5 |
| 0.7 | 3.3 |
| 0.8 | 5.0 |
| 0.9 | 10.0 |
| Note: Model does not include income taxes. | |
![]()
Our treatment of government in the model so far has been, well negligent. We have a government that can spend money, G0, but has no tax revenue. In this section we propose a more complete representation of the government sector by including taxes out of income. This will allow us to consider the potential impact of a change in government fiscal policy that includes either a change in spending, a change in taxes, or both. Adding income tax to the model will change the magnitude of the multiplier but not the general features of the Keynesian model.
First, we propose that government can spend money in one of two ways. The first is autonomous spending, G0. The second is transfer payments such as social security benefits, unemployment benefits, etc.
| Government Spending = G0 + TR | (9) |
We shall also propose the government has two sources of revenues: lump sum taxes and income tax:
| Government Revenues = T0 + t • Y | (10) |
Government fiscal policy represents a change in either spending or taxes. For example, if the economy is in a recession the government could increase autonomous spending, increase transfer payments, reduce lump sum taxes, or reduce the income tax rate. With the Keynesian model we can predict the potential effect of government fiscal policy action on the economy through the multiplier effect.
There is one additional change to the Keynesian model. Consumption is no longer out of total income but out of disposable income. Total income is similar to the gross pay on your paycheck, and disposable income is your take-home pay after taxes have been deducted. The equation for consumption out of disposable income is:
| C = C0 + c • YD |
Disposable income is total income plus government transfer payments less taxes:
| YD = Y + TR - T0 - t • Y |
Thus, the consumption function becomes:
| C = C0 + c • (Y + TR - T0 - t • Y) | (11) |
First, we are given the following equations about how the economy works, which have been described above as equations (1), (11), (5), (6), and (7):
| AE = C + I + G + NX |
| C = C0 + c • (Y + TR - T0 - t • Y) | ||
| I = I0 | ||
| G = G0 | ||
| NX = 0 (for convenience) |
The solution of the model follows the same four steps as earlier.
Step 1. Substitute the equations for the four spending components into the aggregate expenditure equation (1):
| AE = C0 + c • (Y + TR - T0 - t • Y) + I0 + G0 |
Step 2. Apply the equilibrium condition, equation (2):
| Y = AE |
Step 3. Substitute AE from Step 1 into the equilibrium condition in Step 2:
| Y = C0 + c • (Y + TR - T0 - t • Y) + I0 + G0 |
Step 4. Collect the Y terms on the left hand side and solve for national income, Y.
| Y - c • Y + c • t • Y = c • TR - c • T0 + C0 + I0 + G0 |
| (1 - c + c • t ) • Y = c • TR - c • T0 + C0 + I0 + G0 |
| [1 - c • (1 - t )] • Y = c • TR - c • T0 + C0 + I0 + G0 |
| Y = 1 • (c • TR - c • T0 + C0 + I0 + G0) 1 - c • (1 - t ) |
(12) |
The autonomous spending multiplier in equation (12) is slightly different with the introduction of income taxes.
| Autonomous spending multiplier = | 1 1 - c • (1 - t ) |
Income taxes makes the multiplier smaller as shown in Table 5-2.
| Table 5-2. The MPC and Multiplier with Income Taxes | ||
| Marginal Propensity to Consume |
Income Tax Rate |
Autonomous Spending Multiplier |
| 0.8 | 0.0 | 5.0 |
| 0.8 | 0.1 | 3.6 |
| 0.8 | 0.2 | 2.8 |
| 0.8 | 0.3 | 2.3 |
Lump sum taxes (T0) and government transfer payments (TR0) have a slightly different multiplier than the autonomous spending multiplier because of the presence of the marginal propensity to consume, c, in the numerator. Also notice the multiplier on lump sum taxes is negative. An increase in lump sum taxes reduces national income by the amount of the tax increase times the multiplier.
| Government spending: | ΔY = + | 1 1 - c • (1 - t ) |
ΔG0 |
| Lump sum taxes: | ΔY = - | c 1 - c • (1 - t ) |
ΔT0 |
| Transfer payments: | ΔY = + | c 1 - c • (1 - t ) |
ΔTR0 |
A change in lump sum taxes or transfer payments has a smaller effect on aggregate output and national income than a change in government spending.
![]()
Automatic stabilizers are changes in government spending or taxes that reduce the strength of upswings or downswings in economy that occur without any action taken by Congress. Normally you might think of fiscal policy as a stimulus package passed by Congress and signed by the President that might include tax cuts, extension of unemployment compensation, investment tax credits, increased government spending and other fiscal budget changes. But fiscal policy also includes the structure of the government tax and spending system. For example, do you have only lump sum taxes, progressive income taxes, proportional taxes, regressive taxes, and so on.
The structure of the government tax and spending system influences how the government budget responds to the business cycle. The Keynesian model suggests that you want government spending to increase and taxes to decline as the economy moves into a recession. Getting the government to take timely action to implement such changes has become little more than wishful thinking. But the structure of some spending and tax programs can provide the needed stimulus without Congress taking any action. For example, if all taxes were lump sum taxes would tax revenues decline as the economy moves into recession? The answer is no. Income tax revenues on the other hand do fall. When the economy moves into a recession total U.S. income falls and income taxes withheld also declines. Income tax represents an automatic stabilizer while lump sum taxes do not. In Table 5-3 we can see that unemployment compensation and the income tax represent automatic stabilizers while the other listed tax and spending categories do not.
| Automatic Stabilizers - changes in government spending or taxes that reduce the strength of upswings or downswings in demand without any action taken by Congress. |
| Table 5-3. Automatic Stabilizers: unemployment compensation and income tax | |||||
| Economy Moves Into | |||||
| Recession | Inflation | ||||
| Desired Fiscal Policy | |||||
| Government Spending | Increase | Decrease | |||
| Tax | Decrease | Increase | |||
| Actual Outcome | |||||
| Government Spending | |||||
| G0 | Defense Spending | no change | no change | ||
| TR0 | Unemployment Compensation | Increases | Decreases | ||
| TR0 | Social Security Benefits | no change | no change | ||
| Taxes | |||||
| T0 | Lump Sum Tax | no change | no change | ||
| t • Y | Income Tax | Decreases | Increases | ||
![]()
A derivation of the autonomous spending multiplier using algebra was provided above. We can present two other derivations, one based on an infinite geometric series and another using graphical analysis.
With an increase in government spending (ΔG), what is total change in aggregate expenditures (ΔAE)?
Increase in aggregate expenditures, ΔAE(1), represents an increase in income to somebody, ΔY(1) = ΔAE(1). There follows a 2nd round increase in consumption spending out of that income and a further increase in aggregate expenditures:
| 2nd round: ΔAE(2) | = c • ΔY(1) = c • ΔAE(1) = c • ΔG |
| 3rd round: ΔAE(3) | = c • ΔY(2) = c • ΔAE(2) = c • c • ΔG |
Summing an infinite geometric series:
| Multiplier = | 1 1 - c |

Change in national income = AB
Change in autonomous expenditures = CD
Marginal propensity to consume (slope) = BC / AB
By definition the multiplier equals the change in national income divided by the change in autonomous spending, or:
Multiplier = AB / CD
The first step is to recognize that distance CD is equal to BD - BC:
Multiplier = AB / (BD - BC)
Because we have a 45-degree right triangle, distance BD is equal to distance AB:
Multiplier = AB / (AB - BC)
Divide both the numerator and denominator by AB:
| Multiplier = | AB / AB (AB / AB) - (BC / AB) |
Which simplifies to:
| Multiplier = | 1 1 - (BC / AB) |
Since BC / AB represents the slope of the aggregate expenditure function and the marginal propensity to consume as we noted above, then the multiplier is:
| Multiplier = | 1 1 - MPC |
File last modified: August 1, 2004
© Tancred Lidderdale (Tancred@Lidderdale.com)